Aste SLE CA
In questo paragrafo sono descritte le seguenti verifiche allo stato limite di esercizio:
•Stato Limite delle \ di esercizio.
•Stato Limite di fessurazione.
•Stato Limite di deformazione.
•Stato Limite spostamenti sismici.
Verifiche stato limite delle tensioni di esercizio
La verifiche alla tensioni di esercizio sono fatte in accordo a quanto prescritto nel §4.1.2.2.5 delle NTC18.
Tali verifiche vengono effettuate mediante la costruzione dei domini di resistenza considerando il calcestruzzo ancora in fase lineare, ma non reagente a trazione. Nel caso di sollecitazioni quasi permanenti il coefficiente di omogeneizzazione assumerà il valore n = 15 , nel caso di combinazione rara n = Es/Ecm.
In caso di pressoflessione deviata, per le tensioni di esercizio, la formula di verifica utilizzata è [1] :
|My/May| + |Mz/Maz|≤ 1
La tabella di verifica di un beam (trave o pilastro) per le tensioni di esercizio è:

dove:
•x: Ascissa della sezione in esame.
•N-My cem: Tensione del calcestruzzo, per le sollecitazioni N-My, minore della tensione ammissibile.
•N-My steel: Tensione dell'acciaio, per le sollecitazioni N-My, minore della tensione ammissibile.
•N-Mz cem: Tensione del calcestruzzo, per le sollecitazioni N-Mz, minore della tensione ammissibile.
•N-Mz steel: Tensione dell'acciaio, per le sollecitazioni N-Mz, minore della tensione ammissibile.
•N,My,Mz: |My/May|+|Mz/Maz|≤1 risulta vera per ogni combinazione di carico.
Cliccando sui link che compaiono nella colonna x vengono visualizzati i dettagli della verifica della sezione scelta e appare la seguente tabella:

dove sono presenti, tra le altre le seguenti colonne:
•n: coefficiente di omogeneizzazione.
•Myc amm: Momento My ammissibile riferito alla tensione massima del calcestruzzo.
•Mys amm: Momento My ammissibile riferito alla tensione massima dell'acciaio.
•Mzc amm: Momento Mz ammissibile riferito alla tensione massima del calcestruzzo.
•Mzs amm: Momento Mz ammissibile riferito alla tensione massima dell 'acciaio.
•N,My,Mz: risultato della formula di verifica: |My/May| + |Mz/Maz|,
dove May = min{ Myc amm,Mys amm} e Maz = min{ Mzc amm, Mzs amm}
Sezione Circolare
Per la verifica alla tensioni di esercizio, anche coerentemente con quanto fatto per le verifiche agli SLU, nel caso di sezione circolare l'armatura è considerata anulare.
Verifiche stato limite di fessurazione
La verifiche allo stato limite di fessurazione sono fatte secondo quanto indicato nel §4.1.2.2.4 delle NTC18. e §C4.1.2.2.4 della CNTC08. In particolare la deformazione media delle barre e la distanza media tra le fessure sono valutate utilizzando la procedura del D.M. 9 gennaio 1996. (punto B.6 della Circolare Min. LL.PP 252 del 15/10/1996 [5])
La tabella di verifica di un beam (trave o pilastro) per gli stati limiti di fessurazione è:

dove:
•x: Ascissa della sezione in esame.
•N-My: SL di fessurazione verificato per le sollecitazioni N-My.
•N-Mz: SL di fessurazione verificato per le sollecitazioni N-Mz.
•N-My-Mz: SL di fessurazione verificato per le sollecitazioni N-My-Mz.
Cliccando sui link che compaiono nella colonna x vengono visualizzati i dettagli della verifica della sezione scelta e appaiono le seguenti tabelle:

Quattro sono relative alla verifiche dei quattro lati della sezione in presso-tenso flessione retta. I simboli fanno riferimento, oltre che alla NTC e alla CTNC anche alla Circ 252 del 15/10/1996. In particolare:
•β: Come definito al §4.1.2.2.2 delle CNTC18 è il rapporto tra le sollecitazioni N-M effettive e quelle di fessurazione, con variazione proporzionale di N e di M. A seconda del valore di β la si ha:
oβ<0: La sezione risulta interamente compressa.
o0<β<1: La sezione è fessurata.
o1≤β: La sezione ha zone tese ma risulta non fessurata.
Nella Circ 252 del 15/10/1996 e nell'Eurocodice 2 il parametro β viene indicato come (σcr/σs). Data la linearità del secondo stadio, per sezioni inflesse σsr/σs può essere sostituito da Mcr/M[4], per sezioni tese σsr/σs può essere sostituito da Ncr/N[3]. Per sezioni in pressoflessione deviata ponendo:
Ncr= βN; Mxcr= βMx; Mycr= βMy
β si ricava dalla formula:
fctm=β(N/ A - Mx·y/Ix + My·x/Iy)
con la sezione nello stadio 1 (sezione non fessurata) e con , N, Mx ed My le sollecitazioni della sezione.
•σc: Tensione del calcestruzzo, presente se la sezione non è fessurata.
•σs: Tensione dell' acciaio, presente se la sezione è fessurata.
•εsm: Deformazione media unitaria. εsm = σs (1-β1β2β2)/Es con (1-β1β2β2)>0,4, dove
oβ1 = 1 per barre ad aderenza migliorata.
oβ2 = 0,5 nel caso di azioni di lunga durata o nel caso di azioni ripetute.
•Ø: Diametro equivalente delle barre calcolato come indicato nella formula C8.1.18 della CNTC
•s: distanza fra le barre. Se s > 14Ø si adotterà s = 14Ø
•ρ = As/Ac,eff come riportato nella Circ. 252 del 15/10/1996.
•k3: coefficiente che tiene conto della forma del diagramma delle tensioni. (0,125≤k3≤0,25)
•Δsm : distanza media fra le fessure = 2(c+s/10) + k2k3Ø/ρ , dove:
ok2= 0,4 per barre ad aderenza migliorata
oc = ricoprimento dell'armatura
•wd: valore di calcolo di apertura delle fessure. wd = 1,7 Δsm εsm
L'ultima tabella è relativa alla pressoflessione deviata.

Per la verifica a fessurazione in pressoflessione deviata, per ogni combinazione di carico, si procede nel seguente modo:
1.Si sceglie il valore Δsm che corrisponde alla massima fessurazione a pressoflessione semplice. All'autore tale assunzione sembra ragionevole considerando che il calcolo di Δsm viene effettuato con formule semiempiriche anche in pressoflessione semplice. D'altra parte tutta la verifica a fessurazione utilizza formule semiempiriche (e quasi tutti i coefficienti hanno una sola cifra significativa)
2.Si pone wd pari al valore massimo ammissibile (valore nominale w1, w2 o w3 a seconda dei casi) e si ricava εsm dall'equazione:
wd = 1,7 Δsm εsm
3.Si calcola β in pressoflessione deviata.
4.Si ricava σsdall'equazione:
εsm = σs (1-β1β2β2)/Es con (1-β1β2β2) > 0,4
Tale valore σs è la massima tensione dell'acciaio oltre la quale l'apertura delle fessure supera i valori nominali.
5.Ponendo σs amm pari al valore così ottenuto si procede alla verifica utilizzando la disuguaglianza: |My/My| + |Mz/Mz|≤ 1
Nella tabella Verifiche stato limite di fessurazione N-Mx-My sono riportati i risultati di tale verifica, ed in particolare:
•coeff verif : riporta il risultato della formula di verifica: |My/My| + |Mz/Mz| (se >1 la sezione non è verificata)
La verifiche allo stato limite di deformazione sono fatte secondo quanto indicato §C4.1.2.2.2[2] della CNTC. In particolare Il calcolo della deformazione flessionale delle travi è effettuato mediante integrazione delle curvature tenendo conto della viscosità del calcestruzzo.
Il modulo elastico del calcestruzzo Eeff è calcolato tendendo conto degli effetti della viscosità secondo la formula 7.20 EC2:
Eeff = Ecm /(1+φ(∞,t0))
dove:
φ(∞,t0) è calcolato mediate la tabella 11.2.VII delle NTC e con t0 = 30 giorni.
Ecm = Modulo elastico istantaneo del calcestruzzo calcolato con la [11.2.5] delle NTC18.
L'inerzia I* delle sezioni parzialmente fessurate è calcolata con la formula (C4.1.11) della CNTC08. Le sezioni interamente fessurate sono omogeneizzate con n=15.
Lo spostamento è calcolato mediate integrazioni numeriche a partire dai due estremi della trave. Nel caso in cui la trave non sia a sbalzo per ognuna delle 2 integrazioni numeriche effettuate viene calcolata la freccia imponendo lo spostamento complessivo sugli estremi della trave pari a zero. Si procede poi al calcolo della freccia media.
La tabella riassuntiva delle verifiche è la seguente:

sono presenti, tra le altre le seguenti colonne,:
•EI*/EI: = (Eeff I*)/(EcmIca)
dove: Ica = Inerzia della sezione geometrica del solo calcestruzzo
•χ (chi) [1/m]: =Curvatura
•Spost.elast [mm]: Spostamento derivante dell'analisi elastica della struttura (sezioni di solo calcestruzzo interamente reagente).
•coef.Verif:= 250f/L. dove: f= freccia e L = lunghezza trave.
Stato Limite Spostamenti Sismici
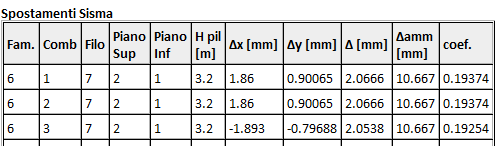
Verifiche per lo stato limite di esercizio in termini di contenimento del danno in caso di sisma fatte come indicato nel § 7.3.6.1 delle NTC18. Vedere la tabella Spostamenti Sisma del paragrafo Verifiche Interpiano.
[1]: Aurelio Ghersi, "Il cemento Armato", 2008, par.6.6, pag.273
[2]: Mezzina-Raffaele-Vitone, "Teoria e pratica delle costruzioni in c.a.-Vol.1 ", 2007, par.12.4.2, pag.554 -(Ed. UTET CittaStudi)
[3]: Cosanza-Manfredi-Pecce, "Strutture in cemento armato ", 2008, par.3.6.2, pag.108
[4]: Aurelio Ghersi, "Il cemento Armato", 2008, par.14.2.6, pag.445
[5]: http://www.ingegnerianet.it/manuale_jasp/stato_limite_fessurazione.pdf
